Developer_kade

• git commit
  • 디렉터리에 있는 모든 파일에 대한 스냅숏을 저장소에 기록하는 것
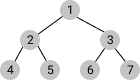
• git branch [branch명]
  • 브랜치란 특정 커밋에 대한 참조 정도로 생각하면 된다.
• git checkout [branch명]
  • 초기에 main브랜치 하나만 있을 때는 사용할 일이 없을 수도 있지만 git branch XXX로 브랜치를 생성했을 때는 여러 브랜치로 이동을 해야 하는 경우가 있다. 이때 사용하는 것이 git chekout [branch명]으로 해당 브랜치로 이동이 가능하다.
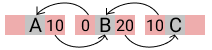
• git merge [끌어올 branch명]
  • 브랜치가 생성이 되고 각 브랜치 별로 커밋작업을 했을때 해당 저장소는 브랜치별로 다른 방향의 이미지가 잡혀있을 것이다.
  • 이때 여러 갈래의 브랜치들을 묶어주는 명령어이다.
  • 부모 브랜치에서 자식을 merge 해주면 된다.
  • 그 뒤에 끌어온 브랜치로 checkout 한 후 부모 branch를 merge 해준다. 이 작업은 자식 브랜치는 부모와 같은 곳을 보고 있지 않으므로 자식 브런치를 부모 쪽으로 끌어오기 위한 작업이다.
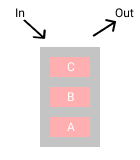
• git rebase [합쳐질 branch명]
  • 커밋들을 모아서 복사한 뒤 다른 곳에 떨궈놓는 작업
  • merge랑 비슷하다
  • 같은 레벨에 브랜치를 가져오기 위해 이전 버전에 있을 다른 브랜치로 이동 후 rebase 해준다.

• Tree
  • 그래프의 일종으로 하나의 노드는 여러개의 노드를 가리킬수 있지만 여러개의 노드가 하나의 노드를 가리킬수 없는 구조이다.
  • 노드와 노드를 이어주는 간선으로 구성되어있다.
  • 트리는 순회가 불가능 하다
  • 용어
    • Root Node : 최상의 부모 노드로서 하나만 존재한다
    • Parent Node : 부모노드, 0개 이상의 자식을 가질 수 있다.
    • child Node : 하나의 부모를 가진다.
    • Leaf Node : 자식이 없는 노드를 말한다.
    • edge : 간선, 노드와 노드를 연결하는 선을 말한다.
    • sibling : 간은 부모를 가지는 형제 노드
    • size : 자신을 포함한 모든 자식(자손)노드의 수
    • depth : 노드의 깊이(부모노드부터 하위 노드까지의 깊이)
    • level : 부모를 0으로 밑으로 내려갈수록 1씩 증가한다.
    • degree : 노드가 가지고있는 edge의 수
  • 
• 종류
  
  • binary : 부모노드가 자식노드를 최대 2개까지 가질 수 있다.
  • full binary : 모든 노드가 2개의 자식을 갖거나 자식이 없는 구조를 말한다.
  • perfect binary
    • 모든 내부 노드가 2개의 자식을 가지고 있어야 함
    • 모든 말단 노드(마지막 레벨에 하나의 노드만 있어서는 안됨)는 같은 높이에 있어야 함
  • ternary : 각 노드가 최대 3개의 자식을 갖는 트리
  • binary search
    • 부모 노드의 왼쪽 자식은 부모의 값보다 작은 값을 지닌 노드로 이루어져 있다.
    • 부모 노드의 오른쪽 자식은 부모의 값보다 큰 값을 지닌 노드로 이루어져 있다.
• Binary Search Tree 구현 코드
  • tree class생성

  • public class BinarySearchTree {
    	Node head = null;
    }​

     
  • 트리구조에서 데이터가 저장될 노드 클래스를 생성한다.

  • public class Node {
    	Node left;
        Node right;
        int data;
    
    	public Node(int data) {
        	this.data = data;
        }
    }

  • 삽입

  • public void add(int data) {
    	if(this.head == null) {
        	this.head = new Node(data);
        } else {
        	Node parentNode = this.head;
            
            while(true) {
            	if(data < parentNode.data) {
                	if(parentNode.left != null) {
                    	parentNode = parentNode.left;
                    } else {
                    	parentNode.left = new Node(data);
                        break;
                    }
                } else {
                	if(parentNode.right != null) {
                    	parentNode = parentNode.right;
                    } else {
                    	parentNode.right = new Node(data);
                        break;
                    }
                }
            }
        }
    }

  • 검색

  • public Node findNode(int data) {
    	if(this.head == null) {
        	return null;
        } else {
        	Node parentNode = this.haed;
            while(parentNode != null) {
            	if(parentNode.data == data) {
                	return parentNode;
                } else if(data < parentNode.data) {
                	parentNode = parentNode.left;
                } else {
                	parentNode = parentNode.right;
                }
            }
            return null;
        }
    }

  • 삭제

  • public Boolean remove(int data) {
    	Node currParentNode = this.head;
        Node currNode = this.head;
    
    	if (this.head == null) {
    		return false;
    	} else {
    		if (this.head.value == value && this.head.left == null && this.head.right == null) {
    			this.head = null;
    			return true;
    		}
    
    		while (currNode != null) {
    			if (currNode.value == value) {
    				searched = true;
    				break;
    			} else if (value < currNode.value) {
    				currParentNode = currNode;
    				currNode = currNode.left;
    			} else {
    				currParentNode = currNode;
    				currNode = currNode.right;
    			}
    		}
    
    		if (searched == false) {
    			return false;
    		}
    	}
    
    
    	if (currNode.left == null && currNode.right == null) {
    		if (value < currParentNode.value) {
    			currParentNode.left = null;
    			currNode = null;
    		} else {
    			currParentNode.right = null;
    			currNode = null;
    		}
    		return true;
    
    	} else if (currNode.left != null && currNode.right == null) {
    		if (value < currParentNode.value) {
    			currParentNode.left = currNode.left;
    			currNode = null;
    	} else {
    		currParentNode.right = currNode.left;
    		currNode = null;
    	}
    		return true;
    
    	} else if (currNode.left == null && currNode.right != null) {
    		if (value < currParentNode.value) {
    			currParentNode.left = currNode.right;
    			currNode = null;
    		} else {
    			currParentNode.right = currNode.right;
    			currNode = null;
    		}
    		return true;
    	} else {
    		if (value < currParentNode.value) {
    			Node changeNode = currNode.right;
    			Node changeParentNode = currNode.right;
    			while (currNode.left != null) {
    				changeParentNode = currNode;
    				changeNode = currNode.left;
    			}
    
    			if (changeNode.right != null) {
    				changeParentNode.left = changeNode.right;
    			} else {
    				changeParentNode.left = null;
    			}
    			changeNode.right = currNode.right;
    			changeNode.left = currNode.left;
    			currNode = null;
    		} else {
    			Node changeNode = currNode.right;
    			Node changeParentNode = currNode.right;
    			while (changeNode.left != null) {
    				changeParentNode = changeNode;
    				changeNode = changeNode.left;
    			}
    
    			if (changeNode.right != null) {
    				changeParentNode.left = changeNode.right;
    			} else {
    				changeParentNode.left = null;
    			}
    			currParentNode.right = changeNode;
    			changeNode.right = currNode.right;
    			changeNode.left = currNode.left;
    			currNode = null;
    		}
    		return true;
    	}
    }​

• Linked List
  • 연결 리스트, 링크드 리스트
  • 노드가 데이터와 포인터를 가지고 있고, 포인터는 다음 노드의 위치를 가지고 있는 구조이다.
  • Single Linked List는 다음 노드를 가리키는 하나의 포인터만 가지고 있다.
    • 
  • Double Linked List는 이전 노드와 다음 노드를 가리키는 포인터를 가지고 있다.
    • 

• 장점
  • 데이터의 삽입과 삭제가 용이하다.
  • 리스트 내에서 자료의 이동이 필요하지 않다.
  • 사용 후 기억 장소의 재사용이 가능하다.
• 단점
  • 포인터 사용으로 인한 저장공간의 낭비가 있다.
  • 알고리즘이 복잡하다.
  • 특정 자료의 탐색 시간이 많이 소요된다.

• 구현 코드(Single Linked List와 Double Linked List가 있지만 본 내용에서는 Double Linked List만 구현하겠다.)
• 어떤 데이터가 들어올지 모르기 때문에 제네릭으로 타입을 잡아서 클래스를 구현했다.
• 노드

  • public class Node<T> {
    	T data;
        Node<T> prev = null;
        Node<T> next = null;
        
        public Node(T data) {
        	this.data = data;
        }
    }

  • 위의 설명에서 Double Linked List의 노드는 앞, 뒤로 포인터를 갖는다고 했다.
  • 노드는 데이터를 가지고 prev로 앞의 노드를 세팅, next로 뒤의 노드를 세팅한다.
• Linked List 클래스 생성
  

  • public class DoubleLinkedList<T> {
    	Node<T> head = null;
        Node<T> tail = null;
    }

• 삽입 메소드 작성

  • public void add(T data) {
    	if(this.head == null) {
        	this.head = new Node<T>(data);
            this.tail = this.head;
        } else {
        	Node<T> node = this.head;
            while(node.next != null) {
            	node = node.next;
            }
            node.next = new Node<T>(data);
            node.next.prev = node;
            this.tail = node.next;
        }
    }

  • 해당 리스트의 head가 null이라면 리스트가 비어있다는 의미이기 때문에 바로 데이터를 삽입해 준다.
  • 이때 head와 tail에 모두 들어온 data를 담은 node를 넣어준다.
  • 만약 head가 null이 아니라면 이미 리스트에 자료가 있기 때문에 리스트를 순회하면서 포인터가 null을 가리키는 곳까지 가서 데이터 삽입 작업을 해준다.
  • node클래스를 보면 내부에 next 필드가 존재함으로 node의 next가 null이 나올 때까지 리스트를 순회하며 null값이 나온다면 그곳에 node를 세팅해 준 후 세팅한 노드의 prev의 포인터를 세팅해 준다.
  • 마지막으로 리스트의 tail을 세팅해준 마지막 노드로 바꿔주면 삽입작업이 끝나게 된다.
• 삭제

  • public Node<T> delete(T data) {
    	if(this.head != null) {
        	Node<T> node = this.head;
            while(node.next != null) {
            	if(node.data == data) {
                	Node<T> prev = node.prev;
                    Node<T> next = node.next;
                    
                    node.prev.next = next;
                    node.next.prev = prev;
                    
                    return node;
                } else {
    				node = node.next;
                }
            }
        }
        
        return null;
    }

  • head가 null이라면 리스트에 아무것도 없기때문에 null을 리턴해 준다.
  • head가 null이 아니라면 리스트를 순회하며 데이터가 같은 값인지를 확인한 후 같은 값이라면 이전 노드와 다음 노드를 연결해서 해당 노드를 끊어낸 후 해당 노드를 반환한다.
• 검색

  • public T frontSearch(T data) {
    	if(this.head != null) {
    		Node<T> node = this.head;
            while(node.next != null) {
            	if(node.data == data) {
                	return node.data;
                } else {
                	node = node.next;
                }
            }
        } 
        return null;
    }
    
    public T tailSearch(T data) {
    	if(this.head != null) {
        	Node<T> node = this.tail;
            while(node != null) {
            	if(node.data == data) {
                	return node.data;
                } else {
                	node = node.prev;
                }
            }
        }
        return null;
    }

  • 검색은 head 혹은 tail부터 검색을 할 수 있다.
  • head는 next를 사용해 순회하면 되고 tail은 prev를 사용해 순회하면 된다.

• MariaDB, MySQL

• DELIMITER $$
  DROP PROCEDURE IF EXISTS loopinsert$$
  CREATE PROCEDURE loopinsert()
  BEGIN
  	DECLARE i INT DEFAULT 1;
      
      WHILE i <= 500 DO
  		INSERT INTO board (
  			board_title
  		) values (
  			concat('제목', i)
  		);
          
          SET i = i + 1;
  	END WHILE;
  END$$
  DELIMITER $$
  
  CALL loopinsert();

• Oracle

• BEGIN
  FOR i IN 1..500 LOOP
  INSERT INTO BOARD(title) 
  VALUES(CONCAT('제목', i);
  END LOOP;
  END;

• 게시판 구축 시에 필요한 기능 중 하나인 검색 기능에 대한 쿼리를 알아보자
• 검색 기능 쿼리 작성 시에도 oracle과 mariadb, mysql은 약간의 차이를 보여준다

• MySQL, MariaDB

• SELECT *
    FROM [테이블 명]
   WHERE [검색 기준 컬럼 명] LIKE concat('%', '[검색할 문자열]', '%')

• Oracle

• SELECT *
    FROM [테이블 명]
   WHERE [검색 기준 컬럼 명] LIKE concat(concat('%', '[검색할 문자열]'), '%')
   
  SELECT *
    FROM [테이블 명]
   WHERE [검색 기준 컬럼 명] LIKE '%'||'[검색할 문자열]'||'%'

MySQL, MariaDB의 경우 concat()을 사용하면 앞뒤로 %를 붙여서 사용이 가능하지만 Oracle은 concat안에 매개변수는 2개밖에 안 들어가기 때문에 concat을 concat으로 감싸주거나 ||를 이용해야 한다.

- Oracle DataBase와 MariaDB, MySql은 페이징 처리를 할 때 사용하는 쿼리가 다르다 코드를 보며 차이점을 확인해 보자

• MariaDB / MySQL

• SELECT *
    FROM [테이블 명]
   ORDER BY [정렬 기준 컬럼] [DESC | ASC]
   LIMIT [시작 행번호] OFFSET [출력 갯수]

• 위와 같이 쿼리의 구조를 잡을 수 있다.
• Mariadb, MySQL은 LIMIT을 통해 출력된 결과물을 원하는 개수만큼 가져올 수 있다.

• SELECT *
    FROM BOARD
   ORDER BY BOARD_IDX DESC
   LEMIT 0 OFFSET 10

• 위의 코드는 게시글 테이블에서 역순으로 정렬 후, 정렬 결과에서 0번부터 10개의 게시물을 가져온다는 쿼리이다.

• Oracle

• SELECT * 
    FROM (SELECT [정렬한 테이블 별칭].*,
  			   rownum rownum_
  		  FROM (SELECT *
  				  FROM [테이블 명]
  				 ORDER BY [정렬 기준 컬럼 명] [DESC | ASC]) [정렬 한 테이블 별칭]) 
    WHERE rownum_ > [시작 행 번호]
  	AND rownum_ <= [끝 행 번호]

• 오라클은 위의 두 데이터베이스보다는 쿼리가 복잡하다.
• LIMIT라는 기능이 없는 것도 있지만 정렬을 먼저 하고 rownum의 조건을 잡을 수 없기 때문이다.
• where절이 실행이 되고 order by절이 실행되는데 순서를 바꿔서 실행할 방법이 없으므로 서브 쿼리를 사용해 정렬을 한 후 rownum과 테이블을 합치는 서브쿼리를 만들어주고 그 뒤에 rownum으로 시작 행부터 끝 행까지를 잡아준다.

• SELECT *
    FROM (SELECT row_.*,
  			   rownum rownum_
  		  FROM (SELECT *
  				  FROM BOARD
  				 ORDER BY BOARD_IDX DESC) row_)
   WHERE rownum_ > 0
     AND rownum_ <= 10

• 다른 방법으로는 아래의 방법을 사용할 수 있다 / ROW_NUMBER()함수와 OVER()함수 사용

• SELECT s.*
    FROM (SELECT ROW_NUMBER() OVER(ORDER BY [정렬 기준 컬럼명] desc) RNUM,
  			   [테이블 alias].*
  		  FROM [테이블 명] [테이블 alias]) s
   WHERE s.RNUM BETWEEN [시작 행] AND [끝 행]

• 인텔리제이에서 깃 헙에 Repository를 생성하고 자료를 올리는 과정을 정리했습니다.

• Stack
  • 위키백과에는 '제한적으로 접근할 수 있는 나열 구조'라고 정의하고 있다.
  • 즉, 한쪽에서만 데이터의 입출력을 할 수 있다
  • 예를 들어서 집의 현관문을 생각해보면 현관문을 통해서만 밖으로 나가거나 집으로 들어올 수 있다.
  • 이와 같은 구조를 Stack이라고 부른다
  • LIFO(Last In First Out)구조라고 부른다.
  • 
• Code
  • 간단하게 구현한 코드이다
  • 편의상 오버플로우나 언더플로우는 작성하지 않았다
  • 큐와 다르게 remove시에 항상 마지막에 있는 값을 빼준다 

  • List<String> stack = new ArrayList<>();
    
    stack.add("A");
    stack.add("C");
    stack.add("D");
    stack.add("B");
    
    System.out.println(stack);
    // A C D B
    
    queue.remove(stack.size() - 1);
    // B out
    queue.remove(stack.size() - 1);
    // D out
    
    System.out.println(stack);
    // A C